国产 肛交

数学念念维才略对孩子来说终点迫切，它波及到逻辑推理、问题不停、轮廓念念维等方面。培养孩子的数学念念维才略不仅有助于他们在学校获得好成绩，还能为他们的畴昔生涯和劳动发展打下坚实的基础。那么，作为家长或教训者，咱们应该如何有用地培养孩子的数学念念维才略呢？

不妨望望英国皇家学会会员、英国沃里克大学数学系荣退教授伊恩•斯图尔特的看法。

撰文 | 伊恩·斯图尔特（Ian Stewart）、戴维·托尔（David Tall）

译者 | 姜喆

数学并非由策画机虚构策画而来，而是一项东说念主类步履，需要东说念主脑基于千百年来的阅历，天然也就伴跟着东说念主脑的一切上风和不及。你不错说这种念念维历程是灵感和遗址的源头，也不错把它行为一种亟待改造的裂缝，但咱们别无取舍。

东说念主类天然不错进行逻辑念念考，但这取决于如何认识问题。一种是认识神志数学讲授每一步背后的逻辑。即便咱们不错查验每一步的正确性，却可能如故无法明白各步如何规划到一说念，看不懂讲授的念念路，想欠亨别东说念主如何得出了这个讲授。

而另一种认识是从全局角度而言的——只要一眼便能领融会盘论证历程。这就需要咱们把想法融入数学的举座章程，再把它们和其他畛域的雷同想法规划起来。这种全面的掌捏不错让咱们更好地认识数学这一举座，并延续卓越——咱们在现时阶段的正证实识很可能会为畴昔的学习打下高超基础。

反之，如果咱们只知说念“解”数学题，而不了解数学学问之间的关系，便无法活泼哄骗它们。

这种全局念念维并非只是为了认识数学之好意思或者启发学生。东说念主类弥远会犯错：咱们可能会搞错事实，可能作念错判断，也可能出现认识偏差。在分步讲授中，咱们可能无法发现上一步推不出下一步。但从全局来看，如果一个裂缝推出了和大标的相背的论断，这一悖论就能领导咱们存在裂缝。

比如，假定 100 个十位数的和是 137 568 304 452。咱们有可能犯策画裂缝，得到 137 568 804 452 这个成果，也可能在写下成果时错抄成 1 337 568 804 452。

这两个裂缝可能皆不会被发现。要想发现第一个裂缝，很可能需要一步局面再行策画，而第二个裂缝却能通过算术的章程减轻地找到。因为 9 999 999 999×100=999 999 999 900，是以 100 个十位数的和最多也只可有 12 位，而咱们写下的却是个十三位数。

不管是策画如故其他的东说念主类念念维历程，把全局认识和分步认识纠合起来是最可能匡助咱们发现裂缝的。学生需要同期掌捏这两种念念维花样，才智完全认识一门学科并有用地实践所学的学问。要分步认识终点通俗，咱们只需要把每一步单独拿出来，多作念熟谙，直到充分认识。全局认识就珍视多，它需要咱们从大皆孤苦信息中找到逻辑章程。

即便你找到了一个得当现时情境的章程，也可能出现和它相背的新信息。有些技术新信息会出错，但已往的阅历也弥远不再适用于新的情境。越是前所未有的新信息，就越可能倜傥于既存的全面认识除外，导致咱们需要更新旧的认识。

1

见解的变成

在念念考具体畛域的数学之前，不错先了解一下东说念主类如何学习新的念念想。因为基础性问题需要咱们再行念念考自认为了解的念念想，是以明白这个学习历程就尤为迫切。每当咱们发现我方并莫得完全了解这些念念想，或者找到尚未探明的基本问题时，咱们就会感到不安。不外大可不必慌乱，绝大部分东说念主皆有过调换的经历。

所非凡学家在刚诞生时皆很稚嫩。这诚然听起来是句空论，却示意了很迫切的一丝——即即是最老练的数学家曾经一步局面学习数学见解。遭受问题或者新见解时，数学家需要在脑海中仔细念念考，回忆已往是否碰到过雷同的问题。这种数学探索、创造的历程可莫得一丝逻辑。

只好当念念绪的齿轮相互啮合之后，数学家才智“嗅觉”到问题或者见解的层次。随后便不错变成界说，进行推导，最终把必要的论据打磨成一个纯粹精妙的讲授。

咱们以“脸色”的见解为例，作念一个科学类比。脸色的科学界说大约是“单色清明映照眼睛时产生的嗅觉”。咱们可不可这样去教孩子。（“安杰拉，告诉我你的眼睛在给与到这个棒棒糖发出的单色光后产生了什么嗅觉……”）当先，你不错先教他们“蓝色”的见解。你不错一边给他们展示蓝色的球、门、椅子等物体，一边告诉他们“蓝色”这个词。然后你再用调换的方法教他们“红色”“黄色”和其他脸色。

一段时分之后，孩子们就会缓缓认识脸色的道理。这时如果你给他们一个没见过的物品，他们可能就会告诉你它是“蓝色”的。接着再教授“深蓝”和“浅蓝”的见解就通俗多了。

叠加这种历程许屡次后，为了建立不同脸色的见解，你还需要再再行来一遍。“那扇门是蓝色的，这个盒子是红色的，那朵毛茛是什么脸色的呢？”如果孩子们能恢复“黄色”，那就诠释他们的脑海中照旧变成了“脸色”这一见解。

孩子们延续成长，延续学习新的科学学问，可能有一天他们就会见到清明透过棱镜变成的光谱，然后学习清明的波长。在经过充足的教授，成为持重的科学家之后，他们就能够精确地说出波长对应的脸色。但对“脸色”见解的精证实识并不可匡助他们向孩子解释“蓝色”是什么。在见解变成的阶段，用波长去澄澈明白地界说“蓝色”是不必的。

数学见解亦然如斯。读者的头脑中照旧建立了大皆的数学见解：解二次方程、绘画像、等比数列乞降等。他们也能熟练地进行算术运算。咱们的方针就是以这些数学认识为基础，把这些见解完善到更复杂的层面。咱们会用读者生涯中的例子来先容新见解。跟着这些见解延续建立，读者的阅历也就延续丰富，咱们就能以此为基础更进一步。

诚然咱们完全不错不借助任何外部信息，用公理化的方法从空集初始构建通盘数学体系，但这对于尚未认识这一体系的东说念主来说险些就是无字天书。专科东说念主士看到书里的一个逻辑构造之后，可能会说：“我猜这是‘0’，那么这就是‘1’，然后是‘2’……这一堆细目是‘整数’……这是什么？哦，我明白了，这细目是‘加法’。”但对于新手来说，这完全就是鬼画符。要想界说新见解，就要用充足的例子来解释它是什么，能用来作念什么。天然，专科东说念主士弥远皆是给出例子的那一方，可能不需要什么认识上的匡助。

2

基模

数学见解就是一组系统的默契——它们源于照旧建立的见解的阅历，以某种花样相互关联。心情学家把这种系统的默契称作“基模”。举例，孩子不错先学习数数（“一二三四五，上山打老虎”），然后过渡到认识“两块糖”“三条狗”的真谛，临了坚韧到两块糖、两只羊、两端牛这些事物存在一个共通点——也就是“2”。那么在他的脑海中，就建立起了“2”这一见解的基模。

这一基模开首于孩子自身的阅历：他的两只手、两只脚，上周在旷野里看到的两只羊，学过的顺溜溜……你会讶异地发现，大脑需要把许多信息归并到一说念才智变成见解或者基模。

孩子们接着就会学习通俗的算术（“假定你有五个苹果，给了别东说念主两个，目下还剩几个”），最终建立起基模，来恢复“5 减 2 是几许”这种问题。算术有着终点精确的性质。如果 3 加 2 等于 5，那么 5 减 2 也就等于 3。孩子们在认识算术的历程中就会发现这些性质，之后他们就不错用已知的事实去推导新的事实。

假定他们知说念 8 加 2 等于 10，那么 8 加 5 就不错认识为 8 加 2 加 3国产 肛交，那么这个和就是 10 加 3，成果是 13。孩子们就这样缓缓地建立了整数算术这一内容丰富的基模。

如果你这时问他们“5 减 6 得几许”，他们可能会说“不可这样减”，或者心想成年东说念主怎样会问这种傻问题，烦懑地咯咯笑。这是因为这个问题不稳妥孩子们脑海中减法的基模——如果我只好 5 个苹果，那不可能给别东说念主 6 个。而在学习过负数之后，他们就会恢复“ -1”。为什么会有这种变化呢？这是因为孩子们原有的“减法”基模为了处理新的见解产生了变化。

在看到了温度计刻度或是了解了银行业务之后，对于“减法”见解的认识就需要改革。在这个历程中，可能仍会心存困惑（ -1 个苹果是什么样的？），但这些困惑最终皆会得到令东说念主舒服的解释（苹果数目和温度计读数存在骨子分别）。

学习历程有很大一部分时分就是让现存的基模变得更复杂，从而能够搪塞新见解。就像咱们刚刚说的，这个历程确乎会伴跟着猜忌。如果能毫无困惑地学习数学该有多好。

然则很灾祸，东说念主不可能这样学习。传闻 2000 多年前，欧几里得对托勒密一生说：“几何学习莫得捷径。”除了坚韧到我方的困惑，了解困惑的成因也很迫切。在阅读本书的历程中，读者将会屡次感到困惑。这种困惑有时源于作家的飘摇，但一般可能是因为读者需要修正个东说念主的默契才智认识更一般的情形。

这是一种拓荒性的困惑，它符号着读者获得了卓越，读者也应当怡然接纳——如果困扰太久那就另当别论了。相似，在困惑得到不停后，一种认识透顶的嗅觉就会伴跟着莫大的情愿鬼使神差，就好像完成了一幅拼图。数学确乎是一种挑战，但这种收场十足调解的嗅觉让挑战成为了雕悍咱们审好意思需求的阶梯。

3

一个例子

发展新不雅念的历程不错用数学见解的发展史来诠释。这段历史本人亦然一种学习历程，只不外它牵连了许多东说念主。负数的引入招致了大皆反对声息：“你不可能比一无通盘更穷了。”但在如今的金融天下，借记和信贷的见解早就让负数融入了日常生涯。

另一个例子是复数的发展。所非凡学家皆知说念，不管是正数如故负数，其平方皆一定是正数。戈特弗里德·莱布尼茨天然也不例外。如果 i 是 -1 的平方根，那么i2=-1，因此 i 既不是正数，也不是负数。莱布尼茨认为它具有一种终点玄妙的性质：它是一个非零数，不大于零，也不小于零。东说念主们因此对于复数产生了庞杂的困惑和不信任感。这种嗅觉于今仍然存在于部分东说念主心中。

复数无法安适地融入大多数东说念主对于“数”的基模，学生们第一次见到它不时也会感到不屈。当代数学家需要借助一个扩展的基模来让复数的存在变得合理。

假定咱们用平庸的花样把实数标在一根轴上：

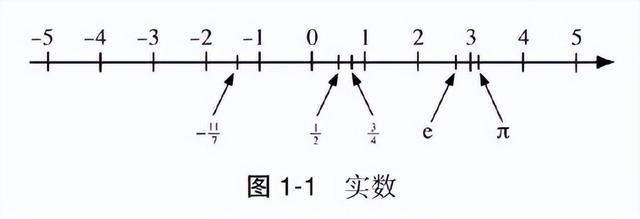
在图 1-1 中，负数位于 0 的左边，正数位于 0 的右边。那 i 在哪？它不可去左边，也不可去右边。那些不接纳复数的东说念主就会说：“这就诠释它哪也不可去。因为数轴上莫得任何地点不错标记 i，是以它不是数。”

然而咱们并非毫无宗旨。咱们不错用平面上的点来走漏复数。（1758 年，弗朗索瓦·戴维认为把虚数画在和实轴垂直的方进取是毫无道理的。幸而其他数学家和他意见相左。）实数位于实轴上，i 位于原点上方一个单元长度的地点。而从原点起程，沿实轴前进 x 个单元，再进取移动 y 个单元（如果 x 和 y 为负数，就朝互异标的移动），就得到了 x + iy 这个数。因为 i 在实轴上方一个单元的地点，而不在实轴上，是以就不可用“i 不存在于实轴上的任何位置”来反对 i 的存在了（见图 1-2）。这样扩展后的基模就能毫无贫困地选定令东说念主不安的复数。

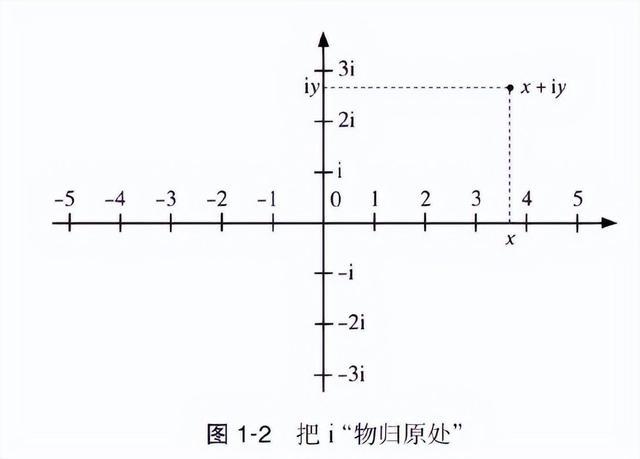
这种作念法在数学中相当常见。当特殊情形被执步履一般情形之后，有些性质依然存在。举例，复数的加法和乘法依然雕悍交换律。但原基模的某些性质（比如关连实数的要领的性质）在执行后的基模（这里指复数的基模）中就不存在了。

这种风物终点普遍，并不限于学生身上，亘古亘今的数学家皆曾有所体验。如果你辩论的畛域业已持重，见解皆得到了解释，况且开发出的方法也足以不停常见问题，那么教学职责就不会很贫困。学生只需要认识道理，莳植熟练度即可。

但如果像是把负数引入用天然数来计数的天下，或是在解方程时遭受复数那样，需要让数学系统发生根人性的变化时，全球皆会感到困惑：“这些新玩意儿是怎样回事？和我想的根底不一样啊！”

这种情况会带来庞杂的灰暗。有些东说念主能坚定地、带着立异念念维选定并掌捏新学问；有些东说念主就只可深陷暴燥，以致对新学问产生反感、不屈的情谊。一个最著名的例子就发生在 19 世纪末期，而它最终也改革了 20 世纪和 21世纪的数学。

4

天然数学与变成数学

数学发源于计数和测量等步履，用于不停现实天下的问题。古希腊东说念主坚韧到绘图和计数有着更为高深的性质，于是他们建立了欧氏几何和质数表面。即便这种柏拉图式的数学追求无缺的图形和数，这些见解仍然是和现实相干联的。这种情状延续了千年。

艾萨克·牛顿在辩论重力和天体开放时，东说念主们把科学称为“天然形而上学”。牛顿的微积分建立在古希腊几何和代数之上，此后者恰是现实中算术运算的执行。

这种基于“现实中发生的事件”的数学持续到了 19 世纪末。其时数学辩论的焦点从对象和运算的性质变成了基于鸠集论和逻辑讲授的神志数学。这种从天然数学到神志数学的历史性过渡包含了视角的彻底改革，也带来了对于数学念念维的长远洞见。它对于从中小学的几何和代数学习向高档教训阶段的神志数学学习的振荡有着至关迫切的作用。

5

基于东说念主类阅历建立神志化见解

跟着数学变得越来越复杂，新见解中有一些是旧学问的执行，有一些则是全新的念念想。在从中学数学过渡到神志数学的历程中，你可能会合计从零初始学习神志化的界说以及如何从基本道理进行神志化的推导才稳妥逻辑。但是已往 50 年的阅历告诉咱们，这种作念法并不理智。

20 世纪 60 年代曾经有东说念主尝试在中小学用全新的方法训诫数学，也就是基于鸠集论和轮廓界说来教授。这种“新型数学”以失败告终。这是因为，诚然众人们能认识轮廓的高明，但是学生们需要一个连贯的学问基模才智认识界说和讲授。

现如今咱们对于东说念主类发展数学念念维的历程有了更长远的相识，因此得以从实验辩论中吸收告诫，来认识为什么学生们对于见解的认识和讲义想进展的真谛有微细偏差。咱们提到这一丝，亦然为了饱读动读者仔细念念考笔墨的准确含义，在见解之间建立邃密的数学关联。

你不错仔细阅读讲授，养成给我方解释的风气。你要向我方解释澄澈为什么某个见解如斯界说，为什么讲授中的前一转不错推出下一转。（参见附录中对于自我解释的部分。）最近的辩论清楚，尝试念念考、解释定理的学生从永远来看会有所得益。曾经有东说念主使用眼部跟踪设备来辩论学生阅读本书第 1 版的花样。辩论发现花更多时分念念考据明的要津法子和在后续锻真金不怕火中获得更高分数是强相干的。咱们锐利推选读者也这样作念，勤奋把学问规划起来能让你建立更连贯的学问基模，让我方永恒受益。

要理智地对待学习历程。在实践中，咱们不老是能够为遭受的每个见解给出精确的界说。比如，咱们可能会说鸠集是“明确界说的一组事物”，但这其实是在袒护问题，因为“组”和“鸠集”在此处有调换的真谛。

在学习数学基础时，咱们要准备好一步一局面学习新见解，而不是一上来就去消化一个严实的界说。在学习历程中，咱们对于见解的认识将愈发复杂。有时，咱们会用严谨的谈话再行陈诉之前不解确的界说（比如“黄色是波长为 5500Å的光的脸色”）。新界说看起来会比作为基础的旧界说好得多，也更具眩惑力。

那一初始就学习这个更好、更有逻辑的界说不就好了吗？其实就怕如斯。

本书的第一部分将从中小学学习过的见解初始。咱们会念念考如何通过标出不同的数一步步建立数轴。这一历程从天然数（1、2、3……）初始，然后是天然数之间的分数，接着咱们延长到原点两侧的正负天然数（整数）和正负分数（有理数），临了扩展到包含有理数和极度数的全体实数。咱们还会蔼然如何天然地进行整数、分数、极少的加减乘除运算，特别是那些将成为不同数系的神志化公理基础的性质。

第二部分将先容得当数学家所使用的讲授见解的鸠集论和逻辑。咱们的训诫将兼顾逻辑的精确性和数学上的洞见。咱们要领导读者，不仅要蔼然界说的内容，还要注意不要因为已往的阅历，就臆断某些性质的存在。比如，学生可能学习过y=x2或者f(x)=sin3x这样能用公式抒发的函数。然而函数的一般界说并不需要公式，只要对于（特定鸠集内的）每一个 x 值，皆存在独一双应的 y 值即可。

这个更一般的界说不仅适用于数，还适用于鸠集。一个被界说的见解所具有的性质必须基于它的界说，用数学讲授的花样推导出来。

第三部分将从天然数的公理和数学归纳法初始，渐渐研讨一系列数系的公理化结构。接着，咱们将展示如何用鸠集论的方法，从基本道理构建出整数、有理数和实数等数系。最终，咱们将得到一系列公理，它们界说了实数系统，包括两种雕悍特定算术蔼然序性质的运算（加法和乘法），以及“完备性公理”。

6

神志化系统和结构定理

这种从尽心挑选的公理构建神志化系统的方法不错进一步执行，从而覆盖更多新的情况。和从日常生涯中繁衍出的系统比拟，这种系统有着庞杂上风。

只要一个定理不错通过神志化讲授从给定的公理推导出来，它在职何雕悍这些公理的系统中就皆建树。不管系统新旧皆是如斯。神志化的定理是不会逾期的。

这些定理不仅适用于咱们熟知的系统，还适用于雕悍给定公理的任何新系统。

这样就没必要一遭受新系统就再行验证我方的不雅念了。这是数学念念维的一个迫切卓越。

另一个不那么显明的卓越在于，神志化系统推导出的某些定理不错讲授，该系统的一些性质使它不错用某种方法图形化，而该系统的另一些性质让它的一些运算不错用标记化方法完成。这样的定理被称为结构定理。比如，任何完备有序域皆领有独一的不错用数轴上的点或者极少来走漏的结构。

这就为神志化讲授带来了全新的功能。咱们不单是是花大皆的篇幅来发展一套自洽的神志化讲授方法，咱们其实发展出了一套交融神志化、图形化和标记化运算的念念维花样，把东说念主类的创造力和神志化方法的精确性纠合了起来。

7

更活泼地使用神志数学

在第四部分，咱们将先容如安在不愁然境下应用这些更活泼的方法。当先咱们会扣问群论，然后会扣问从有限到无限的两种膨胀。一种是把元素个数的见解从有限集执行到无限集：如果两个鸠集的元素逐一双应，就称它们具有调换的基数。基数和旧例的元素个数有许多共通的性质，但它也有一些生疏的性质。

举例，咱们不错从一个无限集（比如说天然数集）中拿走一个无限子集（比如说偶数集），剩下的无限子集（奇数集）和原鸠集有着调换的基数。因此，无限基数的减法和除法无法独一界说。一个无限基数的倒数并不是基数。

那么一个无尽的数在一个系统内有倒数，在另一个系统内却莫得。但仔细念念考之后，咱们就不应该讶异于这些显明矛盾的事实。咱们用来计数的天然数系统原来莫得倒数，有理数和实数系统却有倒数。如果咱们取舍一些性质，执行不同的系统，那么得到不同的执行也不及为奇。

这就得到了一个迫切的论断：数学是延续发展的，看起来不可能的见解可能在一个全新的神志框架下，在合适的公理下就能够建树了。

一百多年前，这种神志化的数学方法缓缓地流行了起来。而菲利克斯·克莱因写下了这样一段话：

“咱们今天对于数学基础的态度，不同于几十年以前；咱们今天可能行为最终原则来叙述的东西，过了一段时分也势必会被超越。”

而在兼并页上他还提到：

“许多东说念主认为教一切数学内容皆不错或必须从新到尾遴荐推导方法，从有限的公理起程，借助逻辑推导一切。某些东说念主想依靠欧几里得的泰斗来致力感触这个方法，但它天然不稳妥数学的历史发展情况。实验上，数学的发展是像树一样的，它并不是有了细细的小根就一直往上长，倒是一方面根越扎越深，同期以调换的速率使枝杈进取生发。撇开比方不说，数学也恰是这样，它从对应于东说念主类正常念念维水平的某一丝初始发展，笔据科学本人的条款及其时普遍的意思意思的条款，有时朝着新学问标的发展，有时又通过对基本原则的辩论朝着另一标的进展。”

本书也将像这样，从学生在中小学所学学问初始，在第二部分深入挖掘基本念念想，在第三部分顶用这些念念想构建数系的神志结构，在第四部分把这些方法应用到更多神志结构上。而在第五部分，咱们对于数学基础的先容将告一段落，转而深入扣问基本逻辑道理的发展，从而辅助读者畴昔在数学方面的成长。